高齢化対応は少子化対策や移民受入ではなく定年変更が正道

少子化と高齢化はともに生産年齢人口比率の低下させ、福祉における「支える人口と支えられる人口の比率」の悪化による支える側の負担増と支えられる側の給付減や¹、経済への悪影響が懸念されている^{2 3}。少子化と高齢化はともにこれを悪化させる原因となるため、まとめて“少子高齢化”として扱われることも多い。しかし、両者は本質的に別の現象であり、高齢化の問題を少子化対策や移民受け入れなど若い世代を増やそうとする対策のみで解決しようとすると破綻する。

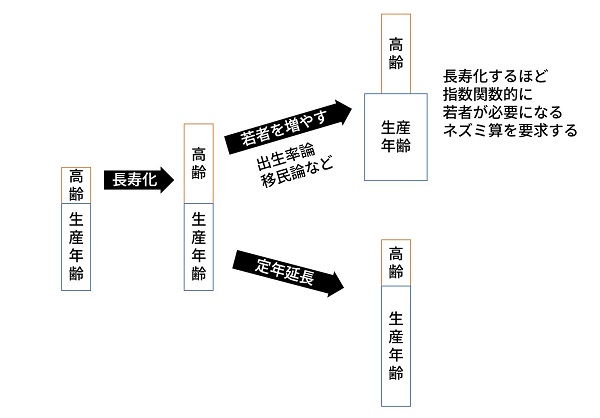
　高齢化によって“支えられる人口”が増えたとき、支える人口と支えられる人口の比を保つには2種類の方法が考えられる。一つは定年を延長することであり、もう一つは若者（生産年齢人口）を増やして“支える人口”を増やすことである。しかし若者を増やしてこの比率を保とうとすると、1歳ごとの人口は若いほど増えねばならず、ネズミ算式に増やす必要が生じてくる。

　この状況をもう少し具体的数字をつけて考えてみよう。子供の増え方は大まかに合計特殊出生率で示すことができる。合計特殊出生率は女性1人が何人子供を産むかを示した数字であり、1世代ごとに人口が(合計特殊出生率/2)倍になると近似することができる。平成26年の第１子出生時の母の平均年齢は年は30.6歳となっており、大まかに30年で人口が(合計特殊出生率/2)倍としてよいだろう。「一定期間後にx倍」といった関係は期間あたり人口増加率を指数とする指数関数で表現することができ、母の平均年齢30歳を繰り込めば　合計特殊出生率＝(年あたり人口増加率)³⁰×2　の形で近似できる。年あたり人口増加率が一定であるとしたうえで、これに働き始め～定年～死亡で区切りをつけて人口ピラミッドとする。

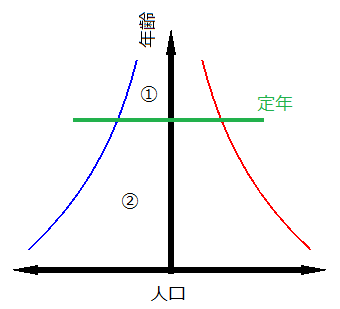
合計特殊出生率を人口増加率とし、指数関数で表現した時の人口ピラミッド。定年後人口①と生産年齢人口②を定積分して解析的に求めることができる。

　このモデルで、20～60歳まで働き、60～80歳が老後として、生産年齢人口:高齢化人口の比率を4:1に保とうとすると、必要となる合計特殊出生率は3.90と計算できる⁴。さすがにこの数字は非現実的と言わざるを得ないだろう。移民を入れるにしても、合計特殊出生率3.90相当のペースで人口を増やしたとなれば人口爆発により早晩居住リソースが尽きるのは明らかであり、マルサスの亡霊を現代に呼び出すだけである。

　このモデルで支える人口と支えられる人口の比率を決定するパラメタは（現代では死亡率は考慮から外してよいものとして）寿命、定年、人口増加率（合計特殊出生率）の3つであり、高齢化問題では寿命の延長が所与のものとなるため、残りのパラメタは定年と合計特殊出生率である。先ほど見た通り合計特殊出生率だけで高齢化を解決するのは非現実的であり、残り一つのパラメタ、定年を操作することを考えよう。定年を操作する場合はシンプルであり、合計特殊出生率が2.0で世代あたり年齢が一定であることを理想形とすれば、20歳から寿命までの期間を支える人と支えられる人の比率で分割するだけでよい。80歳で死ぬとして出生率2.0で支える人口：支えられる人口を4:1に保つ定年は68歳となる。現在の平均寿命は83歳あまりであり、合計特殊出生率2.0を理想とするならば適正な定年は70歳あたりになるだろう。

　以上の議論の通り、高齢化問題を少子化対策や移民で補うのは誤りであると考えられる。少子化対策は少子化対策であり、高齢化対策は定年延長によってなされるのが正しいだろう。また定年延長は現代日本の経済問題への対策としても有望であると筆者は考えているが、それは議論の層が別であり、まず単独で成り立つこの議論のみを示し、経済への影響は別項を立てて考えていく。

(2016/4/22)